Sensor orientation

ENV-548

This file is part of the content downloaded from Sensor orientation.
Course summary

Aircraft with optical and navigation sensors  Objectives
  • To learn the principals of kinematic modeling and estimation of 3D motion with respect to global frames.
  • To understand inertial sensors and develop algorithms for trajectory. determination and sensor orientation via Kalman Filtering .  
  • To be exposed to ‘precise’ (geodetic) approach to sensor integration for mobile mapping,  remote sensing and environmental monitoring.

  support: Polycopies No. 279 Sensor Orientation  (price of paper 100 pages) - PDF via moodle 

         Assistant office hours: during exercises session!

Theory:

  • Overview and course organisation  (see slides introduction)
  • Least-square (LS) estimation (2.2.1), review of main principles on a simple example (black-board)
  • Recursive least-square (RLS) (2.2.2) and how to apply it 
  • Exercises LS / RLS 

Theory:
  • Stochastic processes (5.1) - characteristics (slides with a demo) 
  • Stochastic error models (5.2)  - generations (slides with a demo)
  • Stochastic model identification (5.5) - online demo

BEFORE LECTURE - please read Sec 3.1 and 3.2.1. (4 pages) 

Reference systems:

  • Inertial (i) - please refer to black board notes and lecture notes
  • ECEF(e) - please refer to black board notes and lecture notes
  • Local-level(l) - please refer to black board notes and lecture notes 

Sensors - student presentation

Test 1 (15 %)

Theory on Reference systems (2nd part): 
  • Body frame (b) - please refer to black board notes, lecture notes and slides (attitude)
  • Time derivative of a rotation matrix (black board, slides & lecture notes)

Exercise session: 

  • (1) Rotation matrix time derivative - application for "i" to "e"-frame (solution via video)  
  • (2) Rotation matrix time derivative - application in general frame transformation (solution in pdf) 
  • (3) Preparation for Lab 2 - please read the 3 pages in next week & control it

Preparation: please read the 3 pages  of "Lab2_preparation.pdf" 

Theory:

  • Flowcharts of Navigation equations in the "i" - frame
  • Numerical integration
  • (1-axis attitude "solver") 
Sensors - student presentation

Lab 2 : integration of a nominal signal


Theory:

  • Navigation equations in "e-frame"  
  • Flowcharts of navigation equations in the  "e"-frame  
  • HANDS ON APPLICATION 
Sensors - student presentation
Lab 3: 2D inertial navigation with a realistic signal 



Theory:
  • Attitude initialisation (alignment) - how to perform it ? 
  • Attitude initialisation - effect (impact) of imperfections? 
Sensors  - student presentation

Lab 4 - Attitude initialisation - from real data + sense of Earth "properties" 



Preparation: 

  • Navigation equation in "l-frame"  (Read Chap 6.4+ Chap 6.5)

Theory & Practice of Strapdown Inertial Navigation:
  • 3D Attitude integration 
  • Navigation equation in "l-frame" with a flowchart  (Hint: read Chap 6.4+ Chap 6.5 before)
  • Differences of "l-frame" & "e-frame"
  • Initial alignment - and the rise of Schuler oscilation 
  • Inertial error coupling and surveying procedure with INS 

Exercise session - frames, sensor data, navigation equations and their solutions

Theory:

  • Attitude initialisation (alignment) - how to perform it ? 
  • Attitude initialisation - effect (impact) of imperfections? 
Sensors  - student presentation

Lab 4 - Attitude initialisation - from real data + sense of Earth "properties" 

Theory & Practice of Strapdown Inertial Navigation:
  • 3D Attitude integration 
  • Navigation equation in "l-frame" with a flowchart  (Hint: read Chap 6.4+ Chap 6.5)
  • Differences of "l-frame" & "e-frame"
  • Initial alignment - and the rise of Schuler oscilation 
  • Inertial error coupling and surveying procedure with INS 

Exercise session - frames, sensor data, navigation equations and their solutions


Midterm: 13:15 - 14:00

Theory:

  • Introduction to Kalman Filtering (KF). 
  • KF symbols, terminology and algorithm. 
  • Simple kinematic models in theory & practice - Lab 5(7) 

Theory:

  • Relation between dynamic (F) and transition (PHI) matrices.
  • Numerical evaluation of transition (PHI) and process noise (Q) matrices
  • Linearised and Extended Kalman Filter (EKF)
  • More examples on motion modelling 
  • Sensors 


Theory: 

  • Approaches to integration of satellite and inertial observations - read Chap 8 - satellite positioning first !! 
  • EKF setup for GPS/INS integration read Lab6 - help first !!! 
  • Sensors

Theory:

  • Observability of state vector (for time invariant, F, PHI)
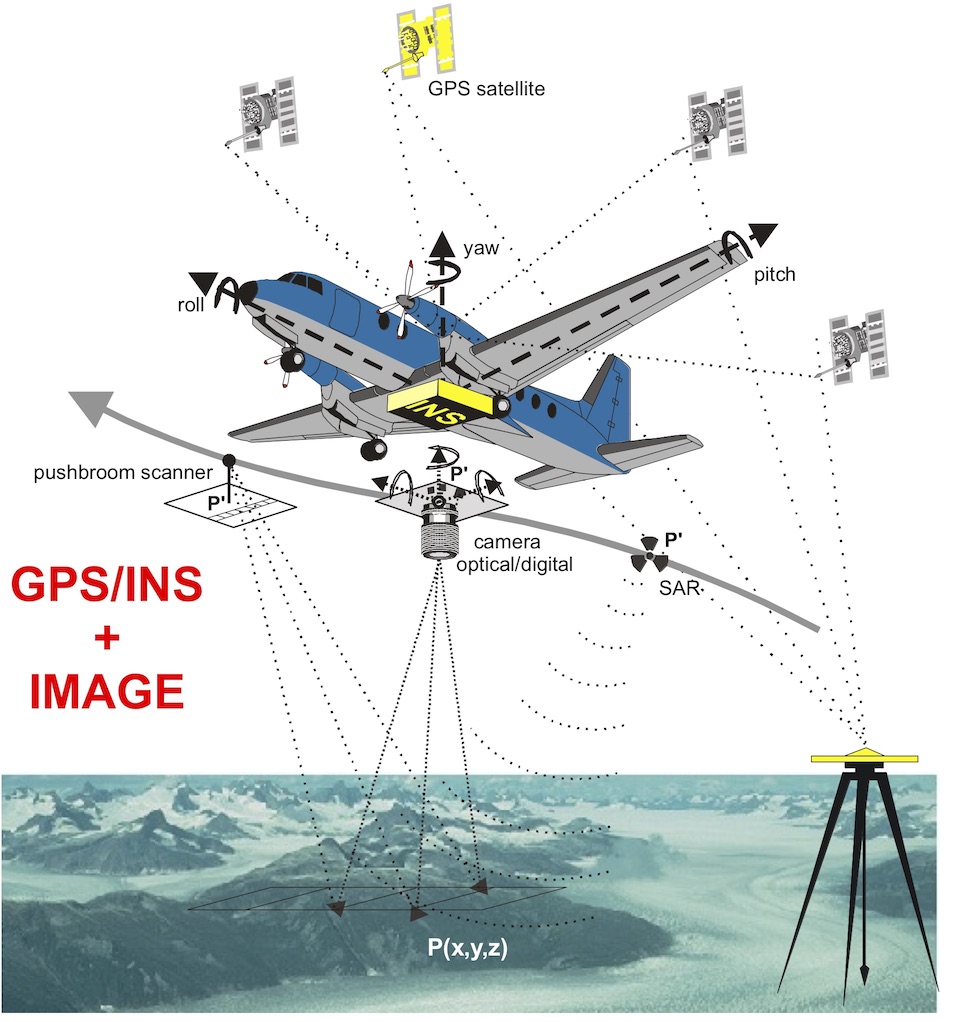
  • Direct and integrated sensor orientation
  • Orientation transformation procedures

  1. EKF Q/A – conceptual & modeling 
  2. How to handle time-correlated measurements in KF/EKF? 
  3. Perspectives: (a) AI/ML in KF, (b) tight-integration of IMU data with optical inputs
  4. Lab 6 in game & over the implementation hurdles