Solution de l’exercice 1¶
Note préliminaire¶
Pour un problème de planification donné, il peut exister différentes façons de le modéliser sous la forme d’un Problème de Satisfaction de Contraintes. Le modèle que nous vous proposons ici correspond à celui qui est décrit dans le chapitre 10.6 du cours. Si, en tentant de modéliser le problème, vous pensez avoir réussi à obtenir un modèle PSC différent qui vous semble valide, nous vous invitons à en discuter avec un(e) assistant(e) pendant la séance d’exercices.
Définition du problème de planification¶
Rappelons qu’un problème de planification est défini par les éléments suivants :
- une liste de propositions qui décrivent l’état du monde
- une liste d’opérateurs qui décrivent les “actions” qui peuvent être exécutées pour changer l’état du monde. Chaque opérateur a des pré- et des postconditions.
- des conditions initiales, décrivant complètement l’état initial du monde en termes de propositions
- des conditions finales, décrivant (complètement ou seulement partiellement) l’état désiré du monde en termes de propositions
- des mutex, qui décrivent des contraintes d’exclusions mutuelles entre les propositions et entre les opérateurs. Les mutex de propositions sont des paires de propositions qui ne peuvent pas être vraies en même temps (par exemple, un missionnaire ne peut pas se trouver sur la rive gauche et sur la rive droite en même temps). Les mutex d’opérateurs définissent les paires d’opérateurs qui ne peuvent pas être exécutés en même temps (par exemple, un même bateau ne peut pas être piloté à la fois par le missionnaire M1 pour transporter le canibale C1 et par M2 pour transporter C2).
Dans notre problème de planification, il y a trois types d‘“acteurs” :
- les bateaux correspondent au type B ; dans notre exemple, il n’y a qu’un seul bateau, dénoté naturellement par B
- les missionnaires correspondent au type M ; il y a deux missionnaires, M1 et M2
- les cannibales correspondent au type C ; il y a deux cannibales, C1 et C2.
Le choix des propositions du problème de planification doit permettre de décrire complètement la position de chaque acteur.
Notre problème présente aussi deux types d‘“actions” possibles :
- traversée du fleuve depuis la rive gauche jusqu’à la rive droite ;
- traversée du fleuve depuis la rive droite jusqu’à la rive gauche.
Chacun de ces deux types d’actions peut faire intervenir un certain nombre d’acteurs. Par exemple, une traversée ne peut avoir lieu qu’à l’aide d’un bateau (i.e. un acteur de type B). Seul un missionnaire (i.e. un acteur de type M) peut conduire le bateau. Le bateau ne peut contenir qu’un passager supplémentaire, qui peut être indifféremment de type M (un missionnaire) ou C (un cannibale). La liste des opérateurs du problème de planification doit couvrir toutes les possibilités de combinaisons d’acteurs pour les deux types d’actions.
Choix des propositions du problème de planification¶
Afin de décrire la position d’un acteur, nous vous proposons d’utiliser deux propositions, correspondant aux deux positions possibles de l’acteur (rive gauche ou rive droite). Pour un acteur A donné, introduisons donc les deux propositions suivantes :
- g(A) est vraie si et seulement si l’acteur A est sur la rive gauche;
- d(A) est vraie si et seulement si l’acteur A est sur la rive droite.
Ces deux propositions peuvent vous sembler redondantes, puisque, si l’acteur A n’est pas sur la rive gauche (g(A) est fausse), alors il est nécessairement sur la rive droite (d(A) est vraie). Nous avons choisi cette représentation car elle se généralise immédiatement à des problèmes un peu plus généraux, dans lesquels il existe plus de deux positions possibles pour un acteur.
Choix des opérateurs du problème de planification¶
Comme indiqué plus haut, des opérateurs vont être nécessaires pour modéliser la traversée du fleuve par des groupes d’acteurs. Pour un état donné, les opérateurs seront les suivants :
- gd(B, M, A) est l’opérateur décrivant la traversée du fleuve de gauche à droite, à bord d’un bateau B, piloté par le missionnaire M, avec pour passager A (qui doit être de type M ou C). Les préconditions de cet opérateur sont que les propositions g(B), g(M) et g(A) doivent être vraies. Les postconditions sont que les propositions d(B), d(M) et d(A) doivent être vraies.
- dg(B, M) est l’opérateur décrivant la traversée de droite à gauche du missionnaire M, à bord du bateau B. Les préconditions de cet opérateur sont que les propositions d(B) et d(M) doivent être vraies. Les postconditions sont que les propositions g(B) et g(M) doivent être vraies.
Remarque : Le choix a été fait dans ce modèle de ne pas tenir compte de la possibilité pour un bateau de faire la traversée de droite à gauche avec un passager (autre que le pilote). Ce choix limite l’éventail de plans valides possibles. Il a l’avantage de correspondre à un problème de planification plus petit, plus facile à résoudre, et qui générera des plans plus courts (puisqu’il n’est pas possible de perdre du temps à faire traverser un cannibale dans un sens, puis dans l’autre sens). Dans notre exemple particulier, sachant que dans l’état initial, les deux cannibales sont sur la rive gauche, il est très facile de constater qu’il existe un plan valide qui ne fait jamais traverser un cannibale de la rive droite à la rive gauche. Dans le cas d’un problème plus général, un tel choix de modèle pourrait générer un problème de planification infaisable, alors même que le problème initial est soluble.
Conditions initiales du problème de planification¶
Initialement, tous les acteurs sont sur la rive gauche. Les conditions initiales sont donc les suivantes:
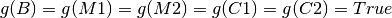
Conditions finales/conditions buts du problème de planification¶
Le but est de faire passer tous les acteurs du côté droit de la rivière. Les conditions finales sont donc les suivantes:
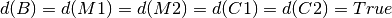
Mutex de propositions du problème de planification¶
Les mutex de propositions sont des paires de propositions qui ne peuvent pas être vraies en même temps. Dans notre problème de planification, pour chaque acteur A, on a le mutex suivant:
![[ g(A), d(A) ]](_images/math/3db040894df678989ecf7356452464aef9e468f9.png)
En effet, un acteur ne peut se trouver en même temps sur la rive gauche et sur la rive droite.
Mutex d’opérateurs du problème de planification¶
Les mutex d’opérateurs dont des paires d’opérateurs qui ne peuvent être exécutés en même temps. Dans notre problème de planification, pour chaque paire d’opérateurs distincts op1 et op2, si les deux opérateurs ont un acteur en commun (qu’il soit de type B, M ou C), alors on a le mutex suivant:
![[ op1, op2 ]](_images/math/6426372dd89688dbf7563600ac1e7198694480c0.png)
Ce mutex traduit le fait qu’un même bateau ne peut pas contenir deux équipages différents en même temps (dans le cas où l’acteur en commun est de type B), et aussi qu’un même missionnaire ou un même canibale ne peut se trouver sur deux bateaux différents en même temps (dans le cas où l’acteur en commun est de type M ou C, et si on a plusieurs bateaux à disposition).
Description du modèle PSC pour le problème de planification¶
Rappelons qu’un plan non linéaire est constitué d’une séquence d’états S0, S1,..., Sn, chaque état Si étant décrit par des propositions qui sont vraies ou fausses au début de l’état, un ensemble d’opérateurs qui sont exécutés pendant cet état, et des propositions qui sont vraies ou fausses à la fin de l’état, après l’exécution des opérateurs (et qui correspondent aux propositions au début de l’état suivant).
Un opérateur est caractérisé par des préconditions (des propositions qui doivent être vraies au début de l’état Si pour que l’opérateur puisse être exécuté) et des postconditions (des propositions qui doivent êtres vraies au début de l’état Si+1 si l’opérateur est exécuté dans l’état Si).
Choix des variables PSC pour les propositions¶
Pour chaque état Si avec i = 0...n+1, et chaque acteur A, le PSC contiendra les variables booléennes suivantes, qui correspondent aux propositions du problème de planification introduites plus haut :
- g(A, Si) = True si et seulement si l’acteur A est sur la rive gauche à la fin de l’état Si-1 / au début de l’état Si ;
- d(A, Si) = True si et seulement si l’acteur A est sur la rive droite à la fin de l’état Si-1 / au début de l’état Si.
Choix des variables PSC pour les opérateurs¶
Pour chaque état Si avec i = 0...n, et chaque opérateur op (par exemple, dg(B, M1)), le PSC contiendra la variable booléenne op(Si) qui indiquera si oui ou non l’opérateur est exécuté dans l’état Si.
Expression des contraintes du PSC¶
Comme indiqué au chapitre 10.6 et plus haut dans cet énoncé, il existe 6 types de contraintes qui doivent être vérifiées pour qu’un plan soit valide :
- les contraintes sur l’état initial
- les contraintes sur l’état final
- les préconditions et les postconditions des opérateurs
- les axiomes de cadre
- les mutex de propositions
- les mutex d’opérateurs
1. Contraintes PSC correspondant aux contraintes sur l’état initial¶
Tous les acteurs sont initialement sur la rive gauche. Par conséquent, les contraintes sur l’état initial prennent la forme très simple suivante :
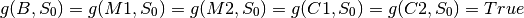
2. Contraintes PSC correspondant aux contraintes sur l’état final¶
Les contraintes sur l’état final sont très comparables aux contraintes sur l’état initial, à la différence fondamentale qu’il faut définir lequel des états S0, S1,..., Sn correspondra à cet état final. En d’autres termes, il faut choisir par avance la longueur des plans solutions que l’on veut considérer (i.e. le nombre total d’états). Si on se restreint à des plans très courts, il est possible qu’on n’obtienne aucune solution, car il n’existe aucun plan qui transforme l’état initial en l’état final avec si peu d’états intermédiaires. Si on permet des plans très longs, la taille du PSC et la complexité de sa résolution explosent. Traditionnellement, on commence donc par se restreindre à des plans courts, et on augmente progressivement la taille des plans si aucune solution n’est trouvée.
Dans notre cas, le problème se résout très facilement à la main, donc on peut tricher et choisir une nombre d’états en sachant qu’il existe un plan solution qui contient ce nombre d’états. Une solution évidente du problème est par exemple la suivante, sachant que le but à atteindre est d’avoir tous les acteurs sur la rive droite :
- gd(B, M1, C1)
- dg(B, M1)
- gd(B, M1, C2)
- dg(B, M1)
- dg(B, M1, M2)
Il suffit donc de 5 étapes, soit 5 états (sans compter l’état initial S0) pour obtenir l’état final désiré. On choisira donc S5 comme état final. Les contraintes sur l’état final sont par conséquent les suivantes :
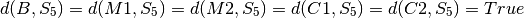
3. Contraintes PSC correspondant aux contraintes de pré- et postconditions des opérateurs¶
Reprenons les deux types d’opérateurs introduits précédemment, et explicitons leurs pré- et postconditions en termes de variables du PSC.
- L’opérateur gd(B, M, A) a pour préconditions que g(B), g(M) et g(A) doivent toutes être vraies. Les postconditions stipulent que d(B), d(M) et d(A) doivent toutes être vraies.
- L’opérateur dg(B, M) a pour préconditions que d(B) et d(M) doivent être vraies. Les postconditions stipulent que g(B) et g(M) doivent être vraies.
Remarque : On n’a pas mentionné ici les “suppressions” de chaque opérateur ; par exemple, une autre postcondition de dg(B, M) est que d(B) doit être fausse. Il n’est pas nécessaire d’expliciter ces postconditions négatives, car elles seront automatiquement imposées par les mutex de propositions introduits précédemment, et présentés en détail plus bas.
En termes de PSC, ces pré- et postconditions prennent la forme des contraintes suivantes sur les variables du PSC, pour chaque état Si avec i = 0...n et chaque opérateur op :
- pour chaque proposition prop qui est une postcondition de l’opérateur op : op(Si) -> prop(Si+1) ;
- pour chaque proposition prop qui est une précondition de l’opérateur op : op(Si) -> prop(Si).
On a utilisé ici la notation -> pour indiquer l’implication logique. Ainsi, si prop est une postcondition de l’opérateur op, alors op(Si) -> prop(Si+1) est équivalent à “si op(Si) = True, alors prop(Si+1) = True”. Ceci traduit bien le fait que si l’opérateur op est exécuté dans l’état Si, alors sa postcondition prop doit être vraie à la fin de l’état Si, c’est à dire au début de l’état Si+1.
4. Contraintes PSC correspondant aux axiomes de cadre¶
Rappelons que les axiomes de cadre stipulent que si aucun opérateur ne vient, dans l’état Si, modifier une proposition prop, alors elle reste identique à l’état Si+1. De manière équivalente : si la valeur d’une proposition change d’un état Si à l’état suivant Si+1, c’est que l’opérateur op(Si) y est pour quelque chose. Par exemple, si g(C1, Si) = True et g(C1, Si+1) = False, alors op(Si) est nécessairement l’un des deux opérateurs suivants : gd(B, M1, C1) ou gd(B, M2, C1).
Remarquez que cette contrainte est de formulation relativement complexe, et qu’en particulier, elle implique plus de 2 variables : prop(Si), prop(Si+1), et les variables pour l’état Si de tous les opérateurs qui ont prop comme pré- ou post-condition. Plus particulièrement, les contraintes d’axiomes de cadre prennent les deux formes suivantes, pour chaque état Si, et pour chaque proposition prop :
- si prop(Si) = False et prop(Si+1) = True, alors pour au moins un opérateur op qui a prop comme postcondition, on a op(Si) = True ;
- si prop(Si) = True et prop(Si+1) = False alors pour au moins un opérateur op qui a prop comme postcondition négative, on a op(Si) = True.
Remarque : Comme indiqué précédemment, il n’est pas nécessaire de considérer le deuxième cas avec la postcondition négative. En effet, prenons l’exemple de la proposition d(M1). Si d(M1) passe de True à False, il n’est pas nécessaire de vérifier que l’opérateur dg(M1) est exécuté, puisqu’alors les contraintes de mutex de propositions imposeront que g(M1) passe (à l’inverse) de False à True, et alors le premier cas ci-dessus suffira pour imposer que dg(M1) soit exécuté.
Rappelons que ces contraintes ne sont pas simplement unaires ou binaires, mais qu’elles ont une multiplicité plus grande que 2. Il va falloir modifier le solveur PSC pour qu’il puisse supporter de telles contraintes.
5. Contraintes PSC correspondant aux mutex de propositions¶
Les mutex de propositions sont les contraintes qui expriment le fait que deux propositions sont MUTuellement EXclusives, c’est à dire qu’elles sont incompatibles et ne peuvent pas être vraies en même temps. Par exemple, on ne peut pas avoir g(M1) et d(M1) vraies en même temps, puisque le missionnaire M1 ne peut pas se trouver à la fois sur la rive droite et sur la rive gauche (à moins que les cannibales l’aient coupé en morceaux).
Plus généralement, pour chaque état Si, et pour chaque acteur A (de n’importe quel type), le modèle PSC contiendra donc les contraintes suivantes :
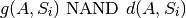
Remarque : Cette contrainte autorise virtuellement qu’un acteur puisse n’être ni sur la rive gauche, si sur la rive droite (g(A, Si) = d(A, Si) = False). Dans la pratique, cette situation ne pourra pas se produire. Ceci peut se démontrer par récurrence. Nous partons du principe que les contraintes sur l’état initial décrivent complètement la situation initiale, c’est à dire qu’au début de l’état 0, un acteur est nécessairement sur une rive donnée. Considérons maintenant l’état k, et supposons qu’un acteur se trouve sur la rive gauche (g(A) = True) au début de cet état (le raisonnement tient toujours si on remplace “gauche” par “droite” et “droite” par “gauche”). On a alors deux possibilités pour les opérateurs exécutés à l’état k : 1) aucun opérateur n’a g(A) comme précondition, et alors les contraintes d’axiomes de cadre vont imposer que g(A) reste vraie à la fin de l’état ; 2) au moins un opérateur a g(A) comme précondition, et alors les contraintes de postconditions vont imposer que d(A) soit vraie à la fin de l’état. Dans les deux cas, la rive sur laquelle se trouve à la fin de l’état est clairement définie.
6. Contraintes PSC correspondant aux mutex d’opérateurs¶
De la même manière que pour les mutex de propositions, chaque mutex d’opérateur [ op1, op2 ] va donner lieu, pour chaque état Si, à la contrainte suivante :
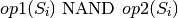
Résumé du modèle PSC¶
Variables¶
- variables booléennes g(A, Si), pour chaque acteur A et chaque état Si ;
- variables booléennes d(A, Si), pour chaque acteur A et chaque état Si ;
- variables booléennes op(Si), pour chaque opérateur op et chaque état Si.
Contraintes¶
- contraintes sur l’état initial :
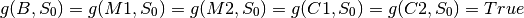
- contraintes sur l’état final :
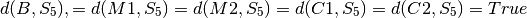
contraintes de pré- et postconditions des opérateurs, pour chaque état Si et chaque opérateur op:
- pour chaque proposition prop qui est une postcondition de l’opérateur op : op(Si) -> prop(Si+1) ;
- pour chaque proposition prop qui est une précondition de l’opérateur op : op(Si) -> prop(Si).
contraintes d’axiomes de cadre, pour chaque état Si et chaque proposition prop :
- si prop(Si) = False et prop(Si+1) = True, alors pour au moins un opérateur op qui a prop comme postcondition, on a op(Si) = True
contraintes de mutex de propositions, pour chaque état Si, et pour chaque acteur A :
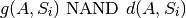
- contraintes de mutex d’opérateurs, pour chaque état Si, et pour chaque paire d’opérateurs distincts op1 et op2 qui ont un acteur en commun :
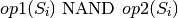
Remarque sur PSC vs SAT¶
Il est intéressant de remarquer que dans ce PSC, toutes les variables sont booléennes. Typiquement, plutôt qu’un résolveur PSC, on utiliserait plutôt un résolveur SAT pour résoudre ce genre de problèmes. Un résolveur SAT est un résolveur spécialisé dans la résolution de problèmes PSC exprimés sous la forme de clauses (des expressions qui peuvent être vraies ou fausses) qui ne portent que sur des variables booléennes.