Clustering¶
Durée estimée : 2 heures.
Objectifs de la série¶
- Implémenter deux algorithmes de clustering.
- Comprendre l’intérêt et les limites de l’apprentissage non supervisé.
Fichiers squelettes¶
Le clustering est une méthode qui permet, à partir d’une base de données, de regrouper les données similaires en agrégats, ou clusters, afin de réduire la complexité apparente des données en découvrant une structure. Les classifications obtenues peuvent ensuite être utilisées pour diverses applications, comme dans les exemples suivants.
- En bioinformatique, des méthodes de clustering peuvent être utilisées pour grouper des espèces d’êtres vivants similaires, en espérant pouvoir généraliser à tout le groupe les propriétés connues d’une espèce particulière. Par exemple, un traitement efficace contre un agent pathogène donné pourrait s’avérer aussi efficace pour d’autres micro-organismes du même cluster.
- Dans le domaine de la vision, le nombre de pixels de différentes nuances de gris dans une image peut être réduit en regroupant plusieurs pixels en un même cluster, et en attribuant une nuance de gris commune à tous les pixels du cluster.
- Une classification d’utilisateurs d’un site internet à partir de leurs habitudes de consultation du site peut permettre de concevoir des interfaces différentes pour chaque classe, afin d’adapter le site aux attentes des utilisateurs. De façon similaire, une classification du contenu d’un site internet peut aussi aider à décider comment diviser le contenu en plusieurs sections thématiques.
Dans cette série d’exercices, nous vous proposons deux domaines particuliers :
- Une liste de maladies, avec leurs symptômes. Une classification de ces maladies devrait permettre d’identifier des groupes d’affections similaires, susceptibles d’être traitées par des traitements similaires.
- Une liste d’entreprises dans le domaine de l’informatique, dont une classification en différents groupes pourrait permettre d’identifier des proches concurrents sur le marché.
Les deux algorithmes de clustering que vous allez implémenter dans les exercices suivants sont des algorithmes itératifs, qui construisent des clusters en suivant l’algorithme général ci-dessous:
Clustering(données)
1. clusters <- initialise_clusters(données)
2. WHILE NOT fini(clusters) DO
3. clusters <- revise_clusters(clusters)
4. END WHILE
5. affiche(clusters)
END Clustering
Exercice 1 : Le clustering de partitionnement k-means¶
L’algorithme k-means part d’une liste de noyaux, qui sont des données autour de chacune desquelles sera construit un cluster. À chaque itération, chaque donnée est réaffectée au cluster du noyau duquel elle est le plus proche, puis chaque cluster est recentré autour d’un nouveau noyau. L’algorithme termine quand l’ensemble des noyaux n’a pas changé d’une itération à la suivante.
La classe Cluster¶
La classe Cluster représente un cluster. Elle contient deux attributs:
elements: la liste des éléments du cluster.kernel: le noyau du cluster (fait aussi partie de la listeelements).
Le constructeur prend un argument kernel: le noyau de départ du cluster. La liste des éléments est initialisée à [kernel].
La méthode principale à implémenter est centre. Elle prend un argument f: la fonction de distance entre deux elements d’un cluster.
Note
La distance est calculée comme le nombre d’entrées différentes dans les listes représentant les éléments à comparer (voir main.py).
La fonction centre met au jour le noyau du cluster afin d’être au “centre” du cluster. Le nouveau noyaux est la donnée qui minimise la moyenne quadratique des distances aux autres données du cluster. En d’autres termes, le noyau xn du cluster C doit minimiser l’expression suivante :
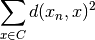
Astuce
A deux reprises, vous allez devoir parcourir une liste pour trouver l’élément de la liste qui minimise une certaine fonction. Ceci peut être implémenté en Python en une seule ligne, grâce à la fonction min(liste, key = fonction), qui prend en paramètres une liste d’éléments, et une fonction que l’on cherche à minimiser. Par exemple, pour retourner l’élément de la liste [1, 2, -3] qui a le plus petit carré, on peut utiliser la ligne de code suivante
min([1, 2, -3], key = lambda x: x**2)
La classe KMeansClustering¶
La classe KMeansClustering implémente l’algorithme k-means. Elle contient quatre attributs:
elements: la liste des éléments à regrouper dans des clusters.k: le nombre des clusters à construire.f: la fonction de distance entre deux éléments.clusters: les clusters construits par l’algorithme k-means.
Le constructeur de la classe prend en argument les éléments a regrouper, le nombre des clusters et la fonction de distance.
Les fonctions principales à implémenter sont initialise_clusters, revise_clusters et clustering.
La fonction initialise_clusters initialise la liste self.cluster de sorte qu’elle contient k clusters avec comme noyaux les k premiers éléments de la liste self.elements. Ensuite, tous les autres éléments sont affectées au premier cluster.
La fonction revise_clusters exécute deux étapes :
- Calcul des nouveaux clusters : initialisation de clusters avec uniquement les kernels, calcul des distances de chaque élément par rapport aux kernels et ajout de l’élément dans le cluster le plus proche.
- Pour chaque cluster ainsi obtenu, le noyau est mis à jour afin d’être au “centre” du cluster. Ceci est implémenté dans la classe
Cluster.
La fonction clustering implémente l’algorithme général ci-dessus. Elle est donc un “wrapper” pour les méthodes initialise_clusters et revise_clusters. Elle initialise les clusters puis les révise de manière itérative jusqu’à ce que les noyaux soient stables (ils ne changent pas d’une itération à l’autre).
Discussion¶
Testez votre algorithme sur les deux exemples fournis : maladies et entreprises. Faites varier le nombre de clusters, ainsi que les noyaux initiaux. Que pensez-vous de la qualité des clusters obtenus? Les données classifiées dans un même cluster sont-elles toujours très similaires ? Est-il facile de choisir le nombre de clusters?
Exercice 2 : Le clustering hiérarchique¶
À la différence du clustering de partitionnement, le clustering hiérarchique par agglomération construit une classification en clusters de plus en plus grands, qui peut se présenter sous la forme d’un dendogramme. La classification hiérarchique obtenue est organisée en groupes et en sous-groupes, afin de discerner les agrégats de similarité grossière des agrégats de similarité plus fine.
L’algorithme part d’un ensemble de clusters réduits à une seule donnée, et, à chaque itération, fusionne les deux clusters les plus similaires. La mesure de similitude entre deux clusters peut être calculée de différentes façons. Dans cet exercice, nous vous en proposons deux: la distance single-link et la distance complete-link. La distance single-link définit la similitude de deux clusters comme la plus courte distance entre deux données de ces clusters. A l’inverse, le complete-link considère la plus longue distance. L’algorithme termine quand toutes les données ont été regroupées en un seul cluster.
La classe Noeud¶
La classe Noeud représente un cluster (un noeud) dans le dendogramme (l’arbre binaire) construit par le clustering hiérarchique. Elle contient trois attributs:
val: la valeur du noeud (Nonesi le noeud n’est pas terminal, une seule donnée si le noeud est feuille).gauche: le noeud à gauche.droite: le noeud à droite.
La fonction fusion permet de fusionner deux noeuds et retourne le nouveau noeud racine.
La fonction valeurs retourne la liste des valeurs contenues dans l’arbre duquel le noeud courant est la racine.
La classe ClusteringHierarchique¶
La classe ClusteringHierarchique implémente le clustering hiérarchique. Elle contient quatre attributs:
elements: la liste des éléments à regrouper dans des clusters.f: la fonction de distance entre deux éléments.lien: le type de distance entre deux clusters (single ou complete).clusters: les clusters construits par le clustering hiérarchique.
Le constructeur de la classe prend en argument les éléments a regrouper, la fonction de distance entre deux éléments, et le type de distance entre deux clusters.
Les fonctions principales à implémenter sont initialise_clusters, revise_clusters, clusters_distances et clustering.
La fonction initialise_clusters initialise la liste self.clusters de sorte qu’elle contient un cluster (un noeud) pour chaque donnée de la liste self.elements.
La fonction revise_clusters cherche les deux clusters c1 et c2 les plus proches et les fusionne en un seul cluster (grâce à la méthode fusion de la classe Noeud). Elle enlève ensuite c1 et c2 de la liste des clusters pour y ajouter le produit de leur fusion. Cette méthode s’aide de la fonction clusters_distances, qui doit retourner une liste contenant les distances entre chaque paire d’éléments des deux noeuds (clusters).
Note
Suivant si la distance entre deux clusters est définie comme le minimum des distances entre chaque paire d’éléments ou comme le maximum, on obtient la distance de type single-link et respectivement complete-link.
La fonction clustering implémente l’algorithme général ci-dessus. Elle est donc un “wrapper” pour les méthodes initialise_clusters et revise_clusters. Elle initialise les clusters puis les fusionne de manière itérative jusqu’à ce que il ne reste qu’un seul élément dans la liste self.clusters (la racine de la hiérarchie construite par le clustering hiérarchique).
Discussion¶
Testez votre algorithme sur les deux exemples fournis : maladies et entreprises. Quelles différences obtenez-vous si vous alternez entre les méthodes single-link et complete-link ? Que pensez-vous de la qualité des clusters obtenus, en comparaison avec l’algorithme k-means?