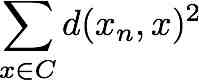
Durée estimée : 2 heures.
Le clustering est une méthode qui permet, à partir d'une base de données, de regrouper les données similaires en agrégats, ou clusters, afin de réduire la complexité apparente des données en découvrant une structure. Les classifications obtenues peuvent ensuite être utilisées pour diverses applications, comme dans les exemples suivants.
Dans cette série d'exercices, nous vous proposons deux domaines particuliers :
Les deux algorithmes de clustering que vous allez implémenter dans les exercices suivants sont des algorithmes itératifs, qui construisent des clusters en suivant l'algorithme général suivant :
FUNCTION clustering( données )Cet algorithme vous est fourni, presque tel quel, dans le fichier clustering.py. Les deux seules différences d'implémentation sont les suivantes :
L'algorithme k-means part d'une liste de noyaux, qui sont des données autour de chacune desquelles sera construit un cluster. A chaque itération, chaque donnée est réaffectée au cluster du noyau duquel elle est le plus proche, puis chaque cluster est recentré autour d'un nouveau noyau. L'algorithme termine quand l'ensemble des noyaux n'a pas changé d'une itération à la suivante.
Comme indiqué dans l'algorithme général de clustering, les fonctions principales à implémenter sont chargeDonnees, fini et reviseClusters.
La fonction chargeDonnees prend deux arguments : le nombre k de clusters désiré, et (en option) une liste de noyaux initiaux. La première partie de cette fonction vous est donnée. Vous devez implémenter la deuxième partie, qui crée la liste CLUSTERS des clusters initiaux. Initialement, CLUSTERS doit contenir k listes de données, la première donnée de chaque liste correspondant au noyau du cluster que la liste représente.
Remarque importante : CLUSTERS doit contenir toutes les données de DONNEES. Celles qui ne sont pas des noyaux devront donc être attribuées à des clusters, d'une manière que vous choisirez et qui n'a pas d'influence sur la trace de l'algorithme. Nous vous proposons par exemple par défaut d'affecter toutes les données (qui ne sont pas des noyaux) au premier cluster.
Codez cette fonction, qui implémente la condition de terminaison de l'algorithme. Elle doit retourner True si et seulement si les noyaux générés à l'itération précédente (et stockés dans la liste VIEUXNOYAUX) sont les mêmes que les noyaux courants.
Indication : Utilisez la fonction retourneNoyaux, que vous devrez préalablement implémenter, et qui retournera la liste des noyaux, générée à partir de la liste des clusters CLUSTERS.
Indication : L'ordre des noyaux dans les listes n'a pas d'importance. La fonction doit retourner True si les deux listes contiennent les mêmes éléments, même s'ils ne sont pas dans le même ordre.
Comme indiqué plus haut, cette fonction exécute deux étapes :
En fixant les noyaux, les clusters sont mis à jour par la fonction formeClusters, que vous devez implémenter. Cette fonction doit retourner une liste de clusters dont les noyaux sont inchangés, mais dont les autres données ont été réaffectées au cluster dont le noyau est le plus proche.
Pour chaque cluster ainsi obtenu, le noyau est mis à jour afin d'être au "centre" du cluster. Cette opération est effectuée par la fonction recentreNoyau, que vous devez implémenter. Cette fonction réordonne les données du cluster afin de mettre en tête de liste la donnée qui minimise la moyenne quadratique des distances aux autres données du cluster. En d'autres termes, le noyau xn doit minimiser l'expression suivante :
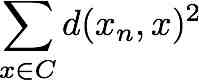
Indication : Utilisez la fonction distance pour calculer la distance entre deux données.
Astuce : A deux reprises, vous allez devoir parcourir une liste pour trouver l'élément de la liste qui minimise une certaine fonction. Ceci peut être implémenté en Python en une seule ligne, grâce à la fonction min(liste, key = fonction), qui prend en paramètres une liste d'éléments, et une fonction que l'on cherche à minimiser. Par exemple, pour retourner l'élément de la liste [1, 2, -3] qui a le plus petit carré, on peut utiliser la ligne de code suivante : min( [1, 2, -3], key = lambda x: x**2 ). Le "key =" est nécessaire pour ne pas que Python interprète le deuxième argument comme un élément à comparer au premier argument. Remarque : ce code ne fonctionne qu'à partir de la version 2.4 de Python. Si vous êtes obligé(e) d'utiliser la version 2.3, vous pouvez utiliser la fonction argmin qui vous est fournie à la place. La ligne de code équivalente sera alors la suivante : argmin( [1, 2, -3], lambda x: x**2 ).
Testez votre algorithme sur les deux exemples fournis : maladies.py et profits.py. Faites varier le nombre de clusters, ainsi que les noyaux initiaux. Que pensez-vous de la qualité des clusters obtenus ? Les données classifiées dans un même cluster sont-elles toujours très similaires ? Est-il facile de choisir le nombre de clusters ?…
A la différence du clustering de partitionnement, le clustering hiérarchique par agglomération construit une classification en clusters de plus en plus grands, qui peut se présenter sous la forme d'un dendogramme. La classification hiérarchique obtenue est organisée en groupes et en sous-groupes, afin de discerner les agrégats de similarité grossière des agrégats de similarité plus fine.
Dans la pratique, l'algorithme part d'un ensemble de clusters réduits à une seule donnée, et, à chaque itération, fusionne les deux clusters les plus similaires. La mesure de similitude entre deux clusters peut être calculée de différentes façons. Dans cet exercice, nous vous en proposons deux : la distance single-link et la distance complete-link. La distance single-link définit la similitude de deux clusters comme la plus courte distance entre deux données de ces clusters. A l'inverse, le complete-link considère la plus longue distance. L'algorithme termine quand toutes les données ont été regroupées en un seul et même cluster.
Comme pour l'algorithme de k-means, les fonctions à implémenter sont chargeDonnees, fini et reviseClusters.
Afin de construire le dendogramme, vous devrez utiliser la classe Noeud, qui représente un noeud du dendogramme, et auquel est associé un cluster. Plutôt que de travailler sur une liste de clusters comme dans l'exercice précédent, vous allez donc travailler sur une liste de noeuds NOEUDS, qui contiendra la liste des noeuds dont le cluster reste encore à fusionner avec un autre cluster.
Implémentez la fonction chargeDonnees, qui initialise cette liste de noeuds, en créant un noeud pour chaque donnée, qui se retrouve donc être son propre cluster. Le constructeur de la classe Noeud prend trois paramètres : la profondeur du noeud dans le dendogramme, la liste des noeuds successeurs (vide pour les noeuds initiaux, qui sont les feuilles du dendogramme), et le cluster associé.
Remarque : La profondeur d'un noeud dans le dendogramme est une mesure du degré de similarité de son cluster. Par exemple, le noeud racine du dendogramme, dont le cluster regroupe toutes les données, aura un degré de similarité le plus faible possible (par convention pris égal à 1). Les feuilles, dont le cluster est réduit à une seule donnée, auront le degré de similarité le plus élevé, égal au nombre total de données. A chaque itération de l'algorithme, la profondeur du noeud créé sera décrémentée d'une unité.
L'algorithme termine après avoir construit la racine du dendogramme. Implémentez ce critère de terminaison, qui sera simplement vérifié lorsque la liste de noeuds NOEUDS ne contiendra plus qu'un seul élément (la racine).
Implémentez la fonction reviseClusters, qui trouve les deux clusters les plus similaires dans NOEUDS, les retire de la liste, les fusionne en un nouveau cluster, et ajoute à la liste NOEUDS un nouveau noeud correspondant.
Indication : Pour mesurer la similitude entre deux clusters, utilisez la fonction distanceClusters, dont vous devrez parfaire l'implémentation.
Astuce : Vous pouvez à nouveau utiliser la fonction min (ou argmin) pour trouver la paire de noeuds dont les clusters sont les plus similaires.
Testez votre algorithme sur les deux exemples fournis : maladies.py et profits.py. Quelles différences obtenez-vous si vous alternez entre les méthodes single-link et complete-link ? Que pensez-vous de la qualité des clusters obtenus, en comparaison avec l'algorithme k-means ?