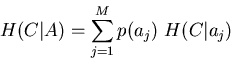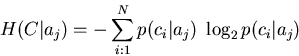Lab 8 : ID3

Durée estimée : 4 heures.

Objectifs de la série

Quel est l'objectif d'ID3
Qu'est-ce que l'entropie dans le cadre d'ID3
Quelles sont les limites inhérentes à tout arbre de décision

Les arbres de décision

Si vous voulez investir dans une compagnie informatique et que vous demandez conseil à un expert financier, celui-ci vous posera toute une série de questions concernant l'entreprise, comme par exemple la concurrence à laquelle elle est soumise, son âge, etc... avant de vous répondre (en admettant qu'il ne connaisse pas déjà l'entreprise). En supposant que vous possédez de nombreux exemples de profils d'entreprises avec la conclusion de l'expert, vous avez à disposition une partie de son expertise qu'il serait intéressant de pouvoir réutiliser sans avoir recours à cet expert lorsque vous voulez analyser de nouvelles entreprises.

Un arbre de décision est une structure qui est souvent utilisée pour représenter des connaissances. Il permet de remplacer un expert humain lorsqu'une caractéristique sur un objet, appelée sa classe par la suite, est désirée. C'est un arbre qui modélise le cheminement intellectuel de l'expert, où :

Chaque noeud intermédiaire correspond à une question sur une propriété de l'objet. Nous appellerons une telle propriété un attribut.
Chaque lien correspond à une valeur de l'attribut.
Chaque noeud terminal correspond à une collection d'objets de même classe, et donc à une classe. Il peut y avoir plusieurs noeuds terminaux différents de même classe.

En parcourant cet arbre (en répondant aux questions des noeuds intermédiaires et en suivant les liens correspondants), vous parvenez à un noeud terminal qui vous renseigne sur la classe de l'objet.

ID3 est un algorithme de construction d'un arbre de décision qui minimise le nombre de "questions" à poser. Il construit l'arbre de décision à partir d'un ensemble d'exemples, c'est à dire d'objets décrits par leurs attributs et leur classe. Son algorithme est le suivant :

FUNCTION ID3( exemples, attributs )
BEGIN
IF exemples est vide THEN
   /* Il n'y a pas d'objet dans cette `sous-classification':
       noeud terminal `spécial' */
   RETOURNER []
ELSE IFtous les objets de exemples font partie de la même classeTHEN
   /* Noeud terminal */
   RETOURNERun noeud contenant tous les objets de exemples
ELSE
   /* Noeud intermédiaire */
    A <- attribut de attributs minimisant l'entropie de la
         classification
    vals <- liste des valeurs possibles pour A
   FOR i IN vals DO
     /* Partitionnement: */
      part[i] <- objets de exemples qui ont i comme valeur pour A
     /* Calcul des noeuds fils: */
      fils[i] <- ID3( part[i], attributs-A )
   ENDFOR
   RETOURNERun noeud avec fils comme successeurs
ENDIF
END ID3

Remarque : Bien évidemment, la qualité de l'arbre de décision construit par ID3 dépend des exemples : plus ils sont variés et nombreux, plus la classification de nouveaux objets sera fiable.

Copiez chez vous le fichier id3_template.py. Celui-ci contient le squelette de votre module ID3.

Voyons cependant les structures de données ainsi que les variables globales dont vous aurez besoin.

Un exemple (un objet avec sa classe) est une liste de la forme :

exemple ::= [val-classe, val-attribut-1, ... val-attribut-k]

où k est le nombre d'attributs. Chaque exemple doit être donné avec une valeur pour chaque attribut. Tous les exemples pour l'apprentissage sont contenus dans la variable globale tousLesExemples (une liste). Afin de "décoder" un exemple, la variable globale attributsEtValeurs est utilisée. Celle-ci est une liste d'attributs donc chaque élément a le format :

attribut ::= [ nom-attribut, valeur-1, ... valeur-m ]

Afin de nous simplifier la vie, nous utiliserons l'index d'un attribut, c'est-à-dire la position de cet attribut dans attributsEtValeurs, au lieu du nom de cet attribut.

Exercice : Écrivez une fonction partition, qui prend deux paramètres : une liste d'exemples exemples et l'index attribut de l'attribut de partition. Elle retournera une liste des partitions selon la valeur de attribut, selon le même ordre que dans attributsEtValeurs. Remarque : si une certaine valeur a_j n'apparaît pas dans exemples, la partition correspondante vaudra [].

Indication : utilisez les fonctions fournies retourneValeurAttribut() et retourneValeursAttribut().

Un noeud de l'arbre de décision est modélisé par une classe Noeud, avec trois champs :

attribut : c'est l'index de l'attribut de partitionnement d'un noeud intermédiaire. Ce champ vaut [] dans le cas d'un noeud terminal.
exemples : c'est l'ensemble des exemples qui "tombent" dans la sous-classification du noeud s'il est terminal. Ce champ vaut [] si c'est un noeud intermédiaire.
enfants : c'est la liste des noeuds fils pour un noeud intermédiaire. Cette liste est ordonnée selon la valeur de l'attribut (champ attribut) : à la i-ième valeur de attribut (selon la variable globale attributsEtValeurs) correspond le i-ième fils. Un fils valant [] indique que l'on n'a pas d'exemple "tombant" dans cette catégorie. Bien entendu, ce champ vaut [] pour un noeud terminal.

Exercice : écrivez une fonction construitArbreDecisionAux() qui accepte deux paramètres : exemples, les exemples de la sous-classification courante, et attributs, la liste des index des attributs encore disponibles pour partitionner les objets. Cette fonction construit un arbre de décision pour les objets de exemples. Aidez-vous du pseudo-algorithme donné ci-dessus.

Indication : utilisez les fonctions meilleurAttribut() pour le choix de l'attribut avec l'entropie la plus faible et partition() pour la partition d'objets selon leur classe.

Entropie

L'entropie est une mesure de l'information, ou plutôt de l'incertitude sur la classification d'un objet. ID3 utilise cette information pour calculer l'arbre de décision le plus petit, ne conservant alors que les informations absolument nécessaires pour classer un objet. Par conséquent, à chaque fois qu'il faut choisir un attribut pour partitionner les exemples, il faut choisir celui qui génère une classification dont l'entropie est minimale. L'entropie H(C|A), soit l'entropie sur la classification après avoir choisi de partitionner les exemples suivant la valeur de l'attribut A, est donnée par l'équation suivante :

(1)

où a_j désigne une valeur de l'attribut A, M le nombre total de valeurs pour l'attribut A et p(a_j) la probabilité que la valeur de l'attribut A soit a_j. En outre :

(2)

où N est le nombre de classes différentes, et p(c_i|a_j) la probabilité conditionnelle qu'un objet soit de la classe c_i étant donné que l'attribut A vaut a_j.

Exercice : écrivez une fonction P_Aj, avec les trois arguments attribut, value et exemples, qui retourne la probabilité que l'attribut d'index attribut valle valeur dans l'ensemble exemples.

Exercice : écrivez une fonction P_Ci_Aj, avec les 4 arguments classe, attribut, value et exemples, qui retourne la probabilité conditionnelle P(classe = classe | attribut = valeur), c'est-à-dire la probabilité qu'un objet soit de la classe classe lorsque l'attribut d'index attribut vaut valeur. Cette probabilité devra être calculée par rapport aux objets de exemples.

Exercice : écrivez une fonction H_C_Aj, avec les trois arguments attribut, value et exemples, qui retourne l'entropie de la sous-classification H(C|a_j), où a_j est la valeur value pour l'attribut d'index attribut. Aidez-vous de l'équation 2. Attention : lorsque p(c_i|a_j) = 0, le résultat de p(c_i|a_j) log₂ p(c_i|a_j) est indéfini : il faut alors prendre la limite et donc p(c_i|a_j) log₂ p(c_i|a_j) = 0.

Exercice : écrivez une fonction entropie(), avec les 2 arguments attribut et exemples, qui retourne l'entropie de la classification des objets de exemples après avoir choisi l'attribut d'index attribut. Aidez-vous de l'équation 1.

Testez ID3

Testez votre module avec les fichiers d'exemples suivants :

profit.py : présente des profils d'entreprises informatiques avec les espoirs de profit.
maladie.py : essaye de trouver de quelles maladies souffre un enfant.

Essayez d'utiliser l'arbre de décision comme un expert humain de manière interactive à l'aide de la fonction classifie().